η τηλεκατευθυνόμενη μπάλα!

Τι κοινό έχουν ο David Beckham, ο Tiger Woods και ο ...Μιχάλης Ρακιντζής;
Όλοι τους έχουν στηρίξει την καριέρα τους στα ...φάλτσα! Κι αν ο τελευταίος τραγουδάει για ένα φάλτσο «μωρό», οι δύο πρώτοι εμφανίζονται στις κορυφαίες θέσεις του καταλόγου με τους πιο πλούσιους αθλητές, χάρη στην ικανότητά τους να επηρεάζουν την πορεία της μπάλας (του ποδοσφαίρου και το γκολφ, αντίστοιχα) χτυπώντας την με ένα χαρακτηριστικό τρόπο στο πάνω ή το κάτω μέρος της.
Αν το καλοσκεφτεί κανείς, το φάλτσο παίζει πρωτεύοντα ρόλο σε όλα τα αθλήματα που παίζονται με μπάλα, είτε πρόκειται για μπιλιάρδο, όπου επιτρέπει στους τεχνικά καταρτισμένους παίκτες να χτυπήσουν μια μπάλα, περνώντας γύρω από εκείνη που τους εμποδίζει, είτε για το μπάσκετ, όπου μια μακρινή πάσα με κατάλληλο φάλτσο μπορεί να φτάσει στον προορισμό της περνώντας την μπάλα πάνω από τον αμυνόμενο και πέφτοντας έγκαιρα στα χέρια του προπορευόμενου επιτιθέμενου στον αιφνιδιασμό - θυμηθείτε τις μαγικές συνεργασίες ανάμεσα στο Γκάλη και το Γιαννάκη!
Το φαινόμενο Magnus

Τι ακριβώς συμβαίνει και η μπάλα σιγά σιγά αρχίζει να παρεκκλίνει από την πορεία της; Πρέπει να θυμόμαστε ότι οι αθλητές χτυπούν τη μπάλα με τέτοιο τρόπο ώστε η θέση του σημείου επαφής (του μπαστουνιού, της στέκας ή του παπουτσιού) με τη μπάλα και η κατεύθυνση του χτυπήματος δεν περνούν από το νοητό κέντρο της;
Όπως περιμένουμε, μετά από το χτύπημα η μπάλα αρχίζει να περιστρέφεται γύρω από το κέντρο της, ενώ παράλληλα κινείται προς τα εμπρός. Η περιστροφή της μπάλας ενεργοποιεί το φαινόμενο Magnus, που πήρε το όνομά του από το Γερμανό φυσικό Heinrich Magnus που το περιέγραψε αναλυτικά στα μέσα του 19ου αιώνα, σχεδόν δύο αιώνες μετά τις πρώτες παρατηρήσεις του Νεύτωνα.
Καθώς λοιπόν η μπάλα περιστρέφεται, η ροή του αέρα γύρω από τη μπάλα παίρνει τη μορφή δίνης, παράλληλα με την κατεύθυνση με την οποία περιστρέφεται η μπάλα. Η πορεία της μπάλας μεταβάλλεται προς το πλάι, επειδή ο αέρας που ακολουθεί την επιφάνεια της μπάλας μέσα σε αυτήν τη δίνη αποσπάται πιο αργά στην πλευρά της μπάλας που κινείται με την ίδια κατεύθυνση με τη δίνη κι έτσι «προλαβαίνει» να σπρώξει τη μπάλα, αφού ο αέρας από την άλλη πλευρά αποσπάται νωρίτερα, δημιουργώντας συνθήκες διαφοράς πίεσης.
Αντίστοιχα, αν χτυπήσουμε τη μπάλα στο κάτω μέρος της (αυτό που στο μπιλιάρδο ή το γκολφ ονομάζεται «πίσω» ή «κάτω φάλτσα») η μπάλα ανυψώνεται πολύ γρηγορότερα. Αυτό έχει σαν αποτέλεσμα να μεταβάλλεται και η συμμετρία του βεληνεκούς της μπάλας: σύμφωνα με τους νόμους της φυσικής και αγνοώντας προς στιγμή την αντίσταση του αέρα, η μπάλα θα έφτανε στο μέγιστο σημείο τροχιάς (το λεγόμενο «ζενίθ») ακριβώς στο μέσο του βεληνεκούς - επειδή όμως στο συγκεκριμένο παράδειγμα, η μπάλα ανυψώνεται και με τη βοήθεια του φαινομένου Magnus.
Έτσι, στην περίπτωση της πάσας του Γιαννάκη προς το Γκάλη, ο οποίος βρίσκεται μερικά βήματα μπροστά από τον (ατυχή...) αμυνόμενο που τον κυνηγάει, η μπάλα ανυψώνεται γρήγορα, περνάει πάνω από τον αμυνόμενο και μετά πέφτει απότομα στα χέρια του Γκάλη, με τα γνωστά αποτελέσματα - αν η μπάλα δεν είχε τα απαιτούμενα φάλτσα, τότε για να μπορέσει να περάσει πάνω από τον αμυνόμενο θα έπρεπε να εκτοξευτεί με τόση δύναμη και να πάρει τέτοια γωνία που δε θα προλάβαινε να πέσει στα χέρια του επιτιθέμενου παίκτη.

Το φάουλ-μπανάνα και οι τερματοφύλακες

Στην περίπτωση του ελεύθερου χτυπήματος (φάουλ) στο ποδόσφαιρο, χτυπώντας τη μπάλα στο δεξί της άκρο και με κατεύθυνση προς τα εμπρός, οι παίκτες αλλάζουν την πορεία της προς τα αριστερά, κάνοντάς την να κινηθεί με τροχιά που έγινε γνωστή σαν «μπανάνα», λόγω του καμπύλου σχήματός της.
Ο Beckham πηγαίνει ένα βήμα παραπάνω: χτυπώντας τη μπάλα στο πάνω μέρος της, την «αναγκάζει» να πέσει από το ζενίθ της γρηγορότερα από το κανονικό και έτσι να δυσκολέψει πολύ τη ζωή του τερματοφύλακα που περιμένει το χτύπημα αφού η μπάλα περνά ξυστά από το πάνω μέρος του ανθρώπινου τείχους, δεν είναι ορατή για ικανό χρονικό διάστημα κι έτσι δεν του δίνει χρόνο να αντιδράσει.

Αν τώρα το πάνω φάλτσο συνδυαστεί και με το πλάγιο φάλτσο ενός χτυπήματος-μπανάνα, έχουμε το πρόσθετο αποτέλεσμα της μπάλας να απομακρύνεται προοδευτικά από τα χέρια του (άτυχου, και πάλι...) τερματοφύλακα, κάνοντας την απόκρουσή της σχεδόν αδύνατη - απλά ρωτήστε τον τότε διεθνή τερματοφύλακα, Αντώνη Νικοπολίδη, για την εμπειρία του στις καθυστερήσεις του αγώνα με την Αγγλία, τον Οκτώβριο του 2001. Γενικά, η δύναμη που περιγράφεται από το φαινόμενο Magnus και η οποία μεταβάλλει την πορεία της μπάλας περιγράφεται από την εξίσωση
Σε αυτήν, σημαντικό ρόλο παίζει η ταχύτητα της μπάλας (συμβολίζεται με V και είναι υψωμένη στο τετράγωνο), αλλά και ο συντελεστής περιστροφής (spin ratio, ανάλογο του Cl) που ορίζεται ως ο λόγος ((γωνιακή ταχύτητα * διάμετρος μπάλας) / (2 * γραμμική ταχύτητα)). Μια «κρυφή» παράμετρος στην παραπάνω εξίσωση σχετίζεται με την επιφάνεια της μπάλας (συμβολίζεται με το Α) που συμμετέχει στο φαινόμενο. Στην πράξη, αυτή επηρεάζεται από τα βαθουλώματα στην επιφάνεια της μπάλας του γκολφ, αλλά και από τη μορφή που έχουν οι ραφές που συνδέουν τα δερμάτινα κομμάτια που απαρτίζουν μια μπάλα ποδοσφαίρου.
Έτσι, κάθε φορά που μια εταιρία αθλητικών ειδών διαθέτει μια καινούρια ποδοσφαιρική μπάλα, οι τερματοφύλακες πρέπει να προσαρμοστούν ταχύτερο δυνατόν στα ...τερτίπια της, ειδικά όταν οι αντίπαλοι ποδοσφαιριστές τη χτυπούν με δύναμη σαν αυτή που ασκεί το πόδι του Roberto Carlos, αφού όπως είπαμε, η ταχύτητα της μπάλας υψώνεται στο τετράγωνο κατά τον υπολογισμό της δύναμης: διαφορετική μορφή και έκταση επιφάνειας έχουν σαν αποτέλεσμα διαφορετικό μέτρο και κατεύθυνση δύναμης ανύψωσης και άρα, διαφορετική πορεία της μπάλας!

Τι να σου κάνει σε ένα δευτερόλεπτο....

Η πρώτη επι­στημονική διερεύνηση της πορεί­ας που ακολουθούν οι μπάλες στον αέρα πραγματοποιήθηκε α­πό τον Νεύτωνα το 1672 στο βι­βλίο του «Νέα θεωρία του φωτός και των χρωμάτων», όπου διερεύ­νησε την απόκλιση της πορείας μιας μπάλας του τένις σε κτύπημα με spin.
Μια πολύ ενδιαφέρουσα νεότερη μελέτη αφορά στο γκολ που σημείωσε ο David Beckham στον αγώνα Αγγλίας -Ελλάδας το 2001. Στην τε­λευταία, κυριο­λεκτικά, στιγμή εκείνου του αγώνα η Αγγλία κέρδισε φάουλ έξω από τη μεγάλη μας περιοχή, ενώ το σκορ ήταν μέχρι εκείνο το λεπτό 1-2 και άφηνε την Αγγλία εκτός των τελικών του Μουντιάλ του 2002. Το εντυπωσια­κό φάουλ που εκτέλεσε ο Beckham έστειλε την Αγγλία στους τελικούς της Ιαπωνίας και της Κο­ρέας. Η μπάλα κατέληξε στα δί­χτυα της ομάδας μας μετά από μια «απρόβλεπτη» πορεία, αφήνοντας εμβρόντητο τον Νικοπολίδη.
Η πορεία της μπάλας από το φάουλ του Beckham αποτέλεσε α­ντικείμενο κοινής ερευνητικής προσπάθειας στα Πανεπιστήμιο του Sheffield (Sports Engineering Research Group) και της Yamamata (Ιαπωνία). Οι ερευνη­τές προσομοίωσαν την πορεία της μπάλας με τη βοήθεια ενός μαθηματικού μοντέλου υπολογι­στικής ρευστομηχανικής (Computational Fluid Dynamics – CFD). Η προσομοίωση έγινε με το μοντέλο CFD Fluent, το ο­ποίο επέλυσε τις εξισώσεις της κίνησης του αέρα γύρω από την μπάλα (δηλαδή της διατήρησης της μάζας, της ορμής και της ενέρ­γειας) και προσδιόρισε το πεδίο ροής, δηλαδή τις γραμμές ροής και τις ταχύτητες του α­έρα γύρω από την μπάλα.
Η επίλυση των εξισώσεων έγινε σε κα­θένα από τα 9 εκατομμύρια ό­γκους, στους οποίους υποδιαιρέθηκε το εξεταζόμενο τμήμα της ροής του αέρα γύρω από την μπάλα. Στην έρευνα χρησιμοποι­ήθηκαν σύγχρονες τεχνικές ανά­λυσης φωτογραφιών και πειρα­ματικές μετρήσεις ροής του αέ­ρα γύρω από μια μπάλα σε αεροσήραγγες.

Πριν περιγράψουμε το φάουλ του Beckham, θα αναφέρουμε δύο σημαντικά χαρακτηριστι­κά της κίνησης μιας μπάλας στον αέρα.
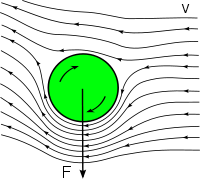
1. Η δύναμη Magnus: Βλέπουμε στο σχήμα μια μπάλα που κινείται στον αέρα (στο σχήμα φαίνονται και οι γραμμές ροής του αέρα), ενώ παράλληλα περιστρέφεται αριστερόστροφα γύρω από έναν άξονα κάθετο στη ροή του αέ­ρα (spin).

Στο σημείο 1 (στα αριστερά τής μπά­λας) η ταχύτητα ροής του αέρα αυξάνεται, με αποτέλεσμα να μειωθεί η τοπική πίεση, σύμφω­να με την εξίσωση Bernoulli.
Το αντίθετο συμ­βαίνει στο σημείο 2 (στα δεξιά της μπάλας), ό­που η ταχύτητα μειώνεται και η πίεση αυξάνε­ται. Η διαφορά πίεσης του αέρα μεταξύ των σημείων 1 και 2 δημιουργεί μια δύναμη στην μπάλα, κάθετα στην κίνηση της (F, δύναμη Magnus), που την ωθεί προς τη μεριά της μι­κρότερης πίεσης (αριστερά), δηλαδή η μπάλα πα­ρεκκλίνει από την ευθύγραμμη πορεία της ακο­λουθώντας τη φορά τής περιστροφής της ή α­πλά «η μπάλα ακολουθεί τη μύτη της».

2. Η δύναμη αντίστασης: Από μετρήσεις που έγιναν σε πειραματικές αεροσήραγγες βρέθηκε ότι η δύναμη αντίστασης που εξασκεί­ται σε μια κινούμενη μπάλα από τον αέρα ε­ξαρτάται από την ταχύτητα της. Όταν η μπάλα έχει μεγάλη ταχύτητα (μεγαλύτερη από περί­που 70 km/h), η ροή του αέρα γύρω από αυτή είναι τυρβώδης (με έντονους στροβιλισμούς του αέρα) και η δύναμη αντίστασης του αέρα στην κίνηση της μπάλας είναι σχετικά μικρή.
Όταν η ταχύτητα της μπάλας είναι μικρή, η ροή είναι στρωτή (σε στρώσεις αέρα, χωρίς στρο­βιλισμούς) και η δύναμη αντίστασης είναι μεγάλη.
Το υλικό της μπάλας, ο αριθμός των τμημά­των της (panels), οποιαδήποτε ασυμμετρία ή α­νωμαλία της επιφάνειας της, όπως π.χ. οι ενώ­σεις των διαφόρων τμημάτων της, μπορεί να ε­πηρεάσουν δραματικά την αεροδυναμική της συμπεριφορά.
Οι μπάλες που χρησιμοποιού­νταν στο παρελθόν είχαν τραχύτερη επιφάνεια και σταθερότερη αεροδυναμική συμπεριφορά, καθόσον η ροή γινόταν στρωτή σε πολύ χαμηλές ταχύτητες κίνησης, οπότε πρακτικά η αντί­σταση τους δεν μεταβαλλόταν σημαντικά κατά την πορεία τους προς το τέρμα και φυσικά δεν ξάφνιαζαν τον τερματοφύλακα.

Ας περιγράψουμε την κίνηση της μπάλας στο φάουλ του Beckham:

1. Η μπάλα τοποθετείται σε απόσταση 26,5m από το τέρμα. Ο Beckham χτυπά την μπάλα με το εσωτερικό του δεξιού του ποδιού (εσωτερικό δεξί φάλτσο) σε ένα σημείο που βρίσκεται σε απόστα­ση 8cm δεξιά από το κέντρο της μπάλας.

2. Το φάλτσο χτύπημα δίνει: (α) μια αρχική ταχύτητα ίση με περίπου 130 km/h και (β) μια πρόσθετη περιστροφική (αριστερόστροφη) κίνηση στην μπάλα (spin). Η μπάλα ανυψώνεται από το έδαφος και κινείται προς το τέρμα, ενώ παράλληλα περιστρέφεται με 8 περιστρο­φές/δευτερόλεπτο. Η περιστροφή αυτή προ­καλεί την καμπύλωση - παρέκκλιση (swerving) της πορείας τής μπάλας προς τα αριστερά (εξαιτίας της δύναμης Magnus). Αρχικά, η ροή του αέρα γύρω από την μπάλα είναι τυρβώδης και η δύναμη αντίστασης του αέρα στην κίνηση της μπάλας είναι μικρή.

3. Η μπάλα περνάει σε απόσταση περίπου 0,50m από το ανθρώπινο τείχος, ακολουθώ­ντας καμπύλη πορεία προς το τέρμα και παράλ­ληλα ανυψώνεται δίνοντας την εντύπωση ότι θα εκτοξευθεί πάνω από το οριζόντιο δοκάρι.
4. Η μπάλα πλησιάζει προς το τέρμα και η ταχύτητα της μειώνεται συνεχώς. Λίγο πριν το τέρμα η ταχύτητα της μπάλας φτάνει τα 67 km/h και η ροή γύρω από την μπάλα γίνεται στρωτή. Τότε, η ροή γίνεται στρωτή και αυξά­νεται σημαντικά η δύναμη αντίστασης του αέρα (150% σε 1 δευτερόλεπτο), αναγκάζοντας την μπάλα να «πέσει» καταλήγοντας στο δεξί Γ της εστίας μας.
Με στοιχειώδεις υπολογισμούς φυ­σικής βρίσκουμε ότι η απόκλιση της μπάλας του «EURO 2008» από την αναμενόμενη ευθεία πορεία της σε ένα καλοχτυπημένο φάλ­τσο φάουλ, με παρόμοια στοιχεία αυτού που αναλύσαμε αυτή μπορεί να φτάσει τα 4m, ξαφνιάζοντας κάθε ανυποψίαστο (;)τερματοφύλακα. Ένα μοντέλο CFD χρειάζε­ται περίπου 2 ώρες για να υπολογίσει ικανοποι­ητικά την πορεία της μπάλας.
Ο Νικοπολίδης θα έχει στη διάθεση του περίπου 1 δευτερόλεπτο για να κάνει τους ίδιους υπολογισμούς χρησιμο­ποιώντας την εμπειρία και το ένστικτο του, στοι­χεία που δεν έχει ο υπολογιστής.

Ο Roberto Carlos και η ...τηλεκατευθυνόμενη μπάλα!
Ένα από τα πιο γνωστά χτυπήματα φάουλ στην ιστορία του επαγγελματικού ποδοσφαίρου ανήκει στο ...μαγικό αριστερό πόδι του Βραζιλιάνου αμυντικού Roberto Carlos. Αν και το ύψος του φτάνει μόλις το 1,68μ., ο ποδοσφαιριστής έχει τέτοια σωματοδομή που του επιτρέπει να δίνει στη μπάλα τέτοια δύναμη, ώστε να μεγιστοποιεί την επίδραση του φαινομένου Magnus, δηλαδή την αλλαγή της πορείας της μπάλας από το φάλτσο.
Στο συγκεκριμένο αγώνα ανάμεσα στις εθνικές ομάδες της Βραζιλίας και της Γαλλίας, ο Carlos παίρνει φόρα για να εκτελέσει ένα φάουλ από ένα σημείο ανάμεσα στο κέντρο του γηπέδου και τη μεγάλη περιοχή της Γαλλίας. Σε ...κανονικές συνθήκες, ένα τέτοιο ελεύθερο χτύπημα δε θα αποτελούσε απειλή για την αντίπαλη εστία - ο Carlos όμως είχε άλλα σχέδια.
Χρησιμοποιώντας μια τεχνική που λέγεται Trivela, o Carlos παίρνει αρκετά μέτρα φόρα, επιταχύνει προς τη μπάλα και τη χτυπά με τα τρία εξωτερικά δάχτυλα του αριστερού του ποδιού. Έτσι, μεγιστοποιεί την ταχύτητα της μπάλας και την επιφάνεια επαφής με το παπούτσι του, δίνοντας αφύσικα υψηλή τιμή στην εξίσωση που περιγράφει το φαινόμενο Magnus.
Έτσι, ενώ ο Fabien Barthez, τερματοφύλακας της εθνικής ομάδας της Γαλλίας σε εκείνο τον αγώνα, περιμένει τη μπάλα να περάσει από τη δεξιά πλευρά του τείχους των αμυντικών, τη βλέπει να περνά από την αριστερή, δηλαδή αυτή που είναι μακριά του, ξεκινώντας μια πορεία που κανονικά θα κατέληγε πολλά μέτρα μακριά από το αριστερό του δοκάρι. Χάρη όμως στη δύναμη του σουτ του Carlos, το φαινόμενο Magnus φέρνει τη μπάλα προοδευτικά προς την εστία και τελικά στα δίχτυα του, εμβρόνητου και ανήμπορου να αντιδράσει, Barthez.
Οι φήμες ότι ό Γάλλος τερματοφύλακας έχασε τα μαλλιά του μετά από αυτόν τον αγώνα ελέγχονται ως αναληθείς!

πηγές
http://www.openscience.gr/node/339
http://tabularasagr.blogspot.com/2008/07/blog-post_16.html